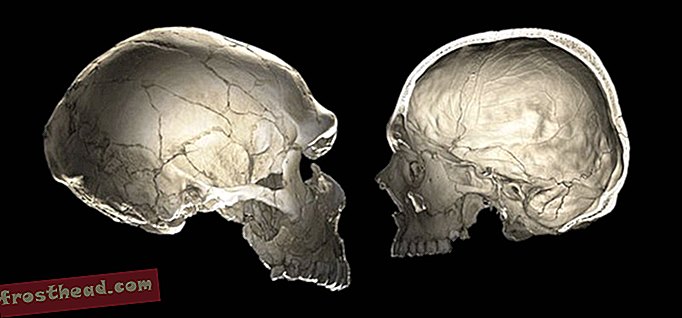
Em 20 de março, o matemático americano-canadense Robert Langlands recebeu o Prêmio Abel, celebrando o sucesso da vida na matemática. A pesquisa de Langlands demonstrou como conceitos de geometria, álgebra e análise poderiam ser reunidos por um link comum para números primos.
Quando o rei da Noruega apresentar o prêmio a Langlands em maio, ele honrará o mais recente em um esforço de 2.300 anos para entender números primos, sem dúvida o maior e mais antigo conjunto de dados em matemática. Como matemático dedicado a este “programa de Langlands”, sou fascinado pela história dos números primos e como os avanços recentes revelam seus segredos. Por que eles cativaram os matemáticos por milênios?
Para estudar primos, os matemáticos esticam números inteiros através de uma malha virtual após a outra até que apenas primos permaneçam. Esse processo de peneiramento produziu tabelas de milhões de primos no século XIX. Ele permite que os computadores de hoje encontrem bilhões de primos em menos de um segundo. Mas a idéia central da peneira não mudou em mais de 2.000 anos.
"Um número primo é aquele que é medido apenas pela unidade", escreveu o matemático Euclid em 300 aC Isso significa que números primos não podem ser divididos por qualquer número menor exceto 1. Por convenção, os matemáticos não contam 1 como um número primo. Euclides provou a infinidade de primos - eles duram para sempre -, mas a história sugere que foi Eratóstenes que nos deu a peneira para listar rapidamente os primos.
Aqui está a ideia da peneira. Primeiro, filtre múltiplos de 2, depois 3, depois 5, depois 7 - os primeiros quatro primos. Se você fizer isso com todos os números de 2 a 100, somente números primos permanecerão.
Preencher múltiplos de 2, 3, 5 e 7 deixa apenas os primos entre 1 e 100. (Cortesia de MH Weissman) Com oito etapas de filtragem, é possível isolar os primos até 400. Com 168 etapas de filtragem, é possível isolar os primos em até 1 milhão. Esse é o poder da peneira de Eratóstenes.
**********
Uma figura inicial na tabulação de primos é John Pell, um matemático inglês que se dedicou a criar tabelas de números úteis. Ele foi motivado a resolver problemas aritméticos antigos de Diofantes, mas também por uma busca pessoal de organizar verdades matemáticas. Graças aos seus esforços, os primos até 100.000 foram amplamente divulgados no início do século XVIII. Em 1800, projetos independentes haviam catalogado os primos em até 1 milhão.
Para automatizar os tediosos passos de peneiramento, um matemático alemão chamado Carl Friedrich Hindenburg usou controles deslizantes ajustáveis para eliminar múltiplos em toda a página de uma tabela de uma só vez. Outra abordagem de baixa tecnologia, mas eficaz, usou stencils para localizar os múltiplos. Em meados do século XIX, o matemático Jakob Kulik tinha embarcado em um projeto ambicioso para encontrar todos os primos até 100 milhões.
Um estêncil usado por Kulik para peneirar os múltiplos de 37. AÖAW, Nachlass Kulik, (Imagem cortesia de Denis Roegel, Autor fornecido) Esse “big data” dos anos 1800 pode ter servido apenas como tabela de referência, se Carl Friedrich Gauss não tivesse decidido analisar os primos por sua própria causa. Armado com uma lista de primos até 3 milhões, Gauss começou a contá-los, um "chiliad", ou grupo de 1.000 unidades, de cada vez. Ele contou os primos até 1.000, depois os primos entre 1.000 e 2.000, depois entre 2.000 e 3.000 e assim por diante.
Gauss descobriu que, à medida que ele contava mais alto, os primos gradualmente se tornaram menos frequentes, de acordo com uma lei do "registro inverso". A lei de Gauss não mostra exatamente quantos primos existem, mas dá uma boa estimativa. Por exemplo, sua lei prevê 72 primos entre 1.000.000 e 1.001.000. A contagem correta é de 75 primos, cerca de um erro de 4%.
Um século depois das primeiras explorações de Gauss, sua lei foi provada no "teorema do número primo". O erro percentual aproxima-se de zero em intervalos de primos cada vez maiores. A hipótese de Riemann, um problema de prêmio de um milhão de dólares hoje, também descreve como a estimativa de Gauss é realmente exata.
O teorema dos números primos e a hipótese de Riemann chamam a atenção e o dinheiro, mas ambos seguem a análise de dados anterior, menos glamourosa.
.....
Hoje, nossos conjuntos de dados vêm de programas de computador em vez de estênceis cortados à mão, mas os matemáticos ainda estão encontrando novos padrões nos primos.
Com exceção de 2 e 5, todos os números primos terminam no dígito 1, 3, 7 ou 9. Nos anos 1800, ficou provado que esses possíveis últimos dígitos são igualmente frequentes. Em outras palavras, se você olhar para os primos até um milhão, cerca de 25% terminam em 1, 25% terminam em 3, 25% terminam em 7 e 25% terminam em 9.
Há alguns anos, os teóricos de números de Stanford, Lemke Oliver e Kannan Soundararajan, foram pegos de surpresa por peculiaridades nos dígitos finais dos primos. Um experimento analisou o último dígito de um primo, bem como o último dígito do primo seguinte. Por exemplo, o primo seguinte depois de 23 é 29: Um vê um 3 e depois um 9 em seus últimos dígitos. Alguém vê 3 e 9 mais frequentemente que 3 e 7, entre os últimos dígitos de primos?
Freqüência de pares de último dígito, entre números primos sucessivos até 100 milhões. As cores correspondentes correspondem a intervalos correspondentes. (MH Weissman, CC BY) Os teóricos dos números esperavam alguma variação, mas o que encontraram superou em muito as expectativas. Os horários são separados por diferentes lacunas; por exemplo, 23 é seis números longe de 29. Mas 3-então-9 primos como 23 e 29 são muito mais comuns que 7-depois-3 primos, embora ambos provenham de um intervalo de seis.
Os matemáticos logo encontraram uma explicação plausível. Mas, quando se trata do estudo de primos sucessivos, os matemáticos são (principalmente) limitados à análise de dados e à persuasão. Provas - o padrão de ouro dos matemáticos para explicar por que as coisas são verdadeiras - parecem décadas à frente.
Este artigo foi originalmente publicado no The Conversation.
Martin H. Weissman, Professor Associado de Matemática, Universidade da Califórnia, Santa Cruz
